ARİTMETİK DİZİ

Ardışık her iki terimi arasındaki farkı eşit olan diziye aritmetik dizi denir.
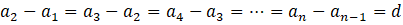
 şeklinde gösterilir.  sayısına aritmetik dizinin ortak farkı denir.
Aritmetik dizinin özellikleri:
1)
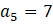
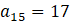
ÖRNEK:   ve   olan aritmetik dizinin 10. terimini bulalım.
ÇÖZÜM:
 
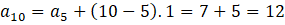
  olarak bulunur.
2)
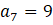
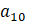
ÖRNEK:    ve    olduğuna göre, değerini bulalım.
ÇÖZÜM:  olduğundan;
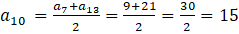
 olarak bulunur.
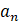
3)  aritmetik dizisinde ilk n terim toplamı
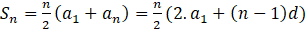
  formülü ile hesaplanır.
ÖRNEK: 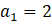  ve ortak farkı  olan artan aritmetik dizide ilk 16 terimi toplamını bulalım.
ÇÖZÜM:
GEOMETRİK DİZİ
Ardışık her iki terimi arasındaki oranı eşit olan diziye geometrik dizi denir.
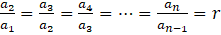
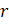
 şeklinde gösterilir.  sayısına geometrik dizinin ortak çarpan denir.
Geometrik dizinin özellikleri:
1)    
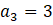
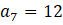
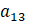
ÖRNEK:   ve    olan geometrik dizide  değerini bulalım.
ÇÖZÜM:
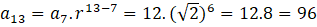
 bulunur.
 2)  
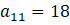
ÖRNEK:   ve    olan geometrik dizide  8. terimi bulalım.
ÇÖZÜM: 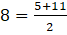 olduğundan;
 
3)  geometrik dizisinde ilk n terim toplamı
 
ÖRNEK: İlk terimi 3 ve ortak çarpanı 2  olan terimin ilk 8 teriminin toplamını bulalım.
ÇÖZÜM:  
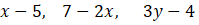
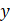
ÖRNEK:  ifadeleri hem aritmetik hem de geometrik dizinin ardışık üç terimi olduğuna göre  ve  değerlerini bulalım.
ÇÖZÜM: Bir dizi hem aritmetik hem de geometrik dizi ise dizi sabit dizi olmalıdır.
 

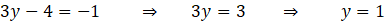
  bulunur.